Dimensional Aspects of the Efimov Physics

par Dr Derick dos Santos Rosa (ITA)

jeudi 5 sept. 2024, 14:00 → 15:00 Europe/Paris

100/0-A018 - Salle Library (IJCLab)

We solved the three-body mass-imbalanced problem embedded in D dimensions for zero-range resonantly interacting particles. We derived the negative energy eigenstates of the three-body Schrodinger equation by imposing the Bethe-Peierls boundary conditions in D-dimensions for zero-energy two-body bound states. The solution retrieves the Efimov-like discrete scaling factor dependence with dimension. The analytical form of the mass-imbalanced three-body bound state wave function is used to study the single-particle momentum distribution of mass-imbalanced Efimov states embedded in noninteger dimensions. The contact parameters, which can be related to the thermodynamic properties of the gas, were calculated from the high momentum tail of the single particle densities. We studied the dependence of the contact parameters with the progressive change of the noninteger dimension. We found that the two- and three-body contacts grow significantly in magnitude with the decrease of the noninteger dimension, impacting observables of resonantly interacting trapped Bose gases. At the end, I discuss about the signature of an unatomic system which is revealed by a continuous scale invariance that appears during a progressive dimensional squeezing of a resonantly interacting trimer
 

---

How to reach the seminar room:

Whereabouts of the laboratory on the Paris-Saclay campus

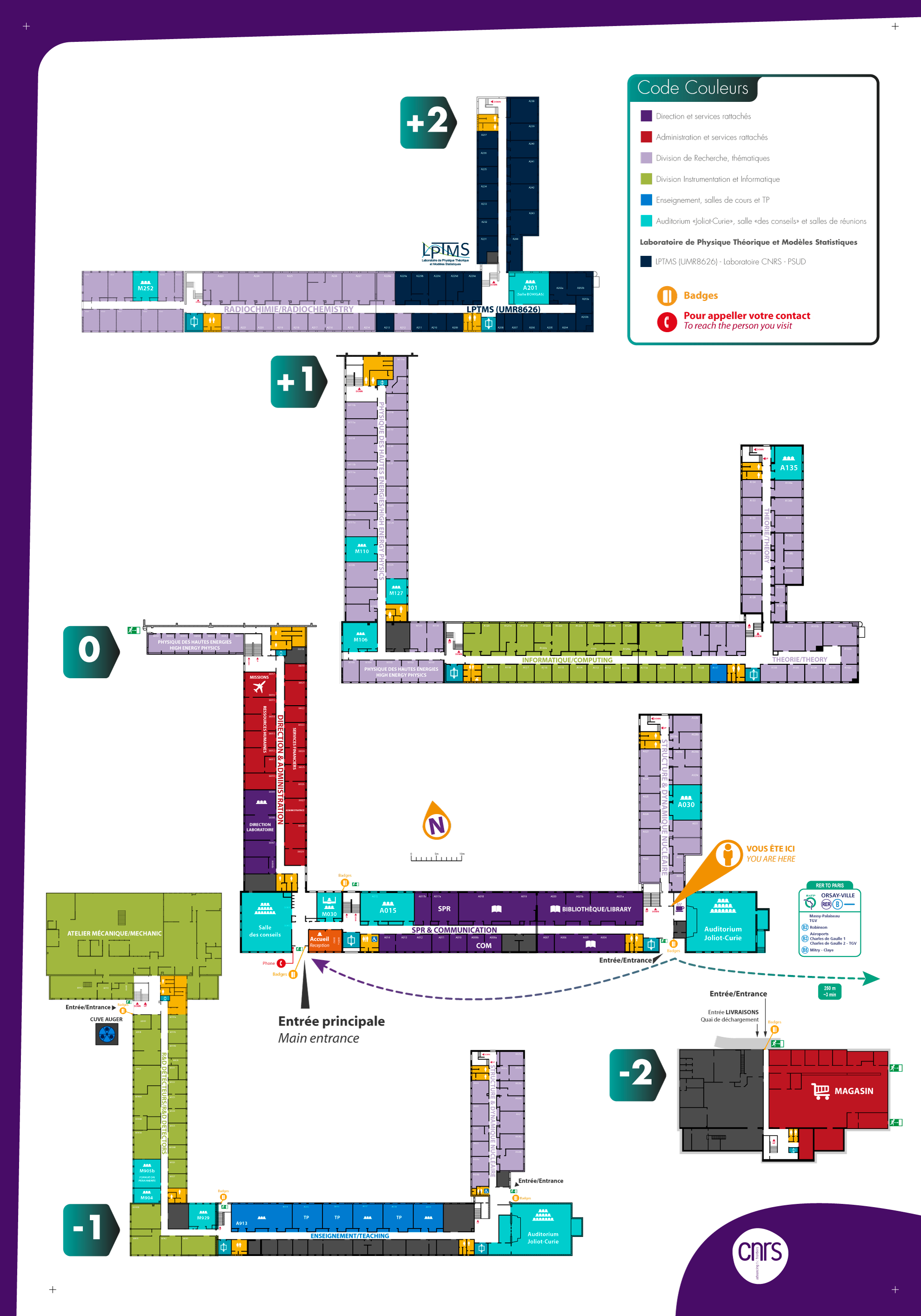
Bat. 100, general room map

Abstract.pdf

DIMENSIONAL ASPECTS.pdf