Séminaires
Mean-field approximation on steroids: exact description of the deuteron
par
→
Europe/Paris
100/0-A018 - Salle Library (IJCLab)
Description
In this work, we investigate the possibility to describe the deuteron, the lightest bound nuclear system made of a single proton and a single neutron, within a mean-field-based framework. At first glance, this endeavor might appear paradoxical as such a two-body system does not warrant, a priori, the use of a mean-field approximation. Nevertheless, we demonstrate that by enriching the mean-field description through the addition of symmetry-breaking and -restoration techniques, it is possible to obtain an exact description of the deuteron within a scheme that, for all intents and purposes, conserves a mean-field complexity.
More precisely, we show that the variation after particle-number projection exploring the space of Bogoliubov quasi-particle states is able to perfectly reproduce the deuteron binding energy as well as the expectation value for the other observables characterizing its 1+ ground state. A key condition to achieve this correct description is the inclusion of proton-neutron pairing through the mixing of proton and neutron single-particle states in the Bogoliubov reference states.
Interestingly, the results presented in this work illustrate in the case of a finite system the known fact that the neutron-proton BCS equation becomes equivalent to the Schrödinger equation for the deuteron in low-density symmetric nuclear matter.
How to reach the seminar room:
Whereabouts of the laboratory on the Paris-Saclay campus
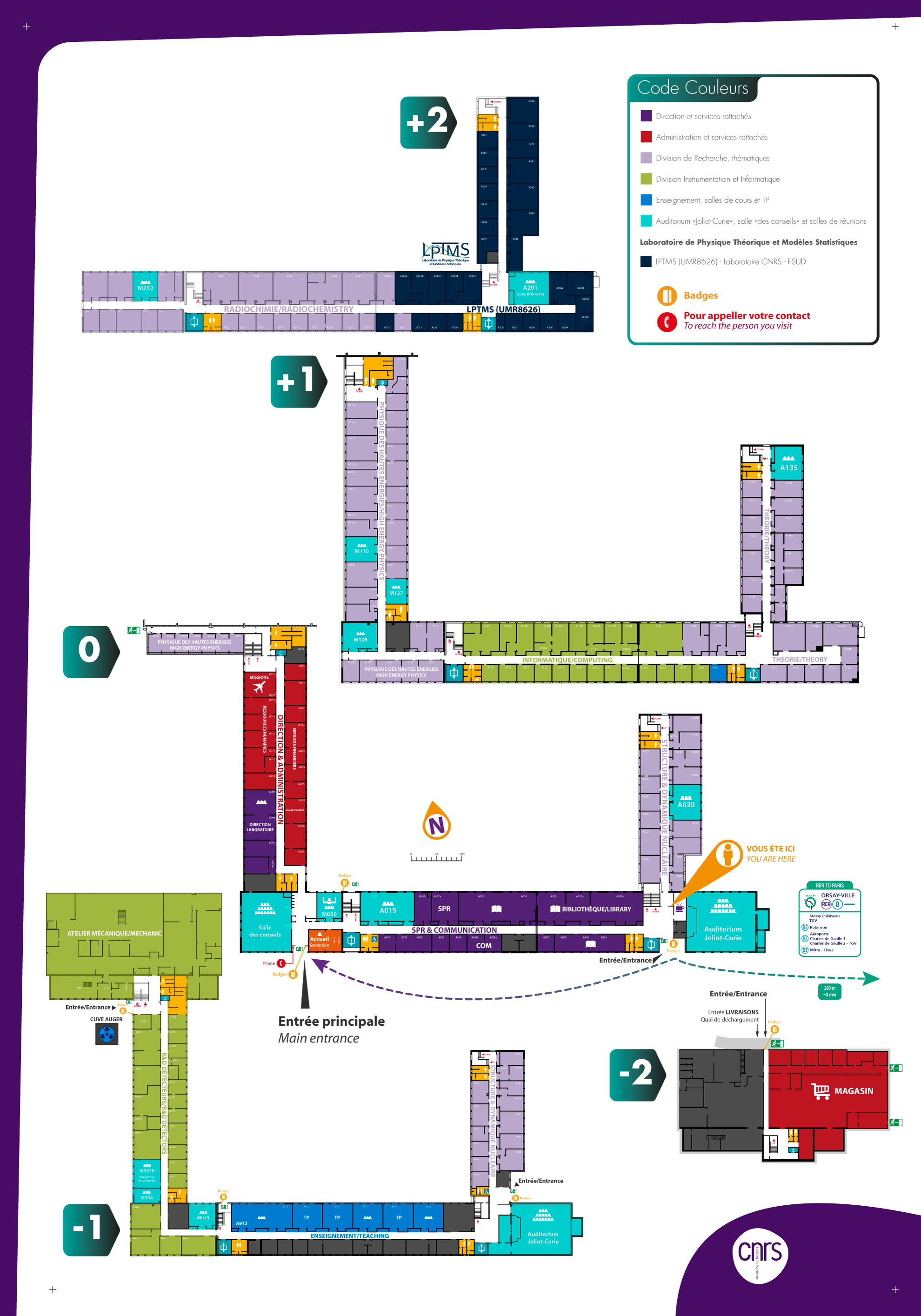
Bat. 100, general room map
Organisé par
G. Hupin
Participants
54
ID de réunion Zoom
99403008084
Hôte
Guillaume Hupin
Hôte alternatif
Pierre Arthuis
URL Zoom
