Nuclear shape phase transitions: From analytical models to quantum computing approaches

par Samira Baid (University of Seville)

jeudi 10 avr. 2025, 14:00 → 15:00 Europe/Paris

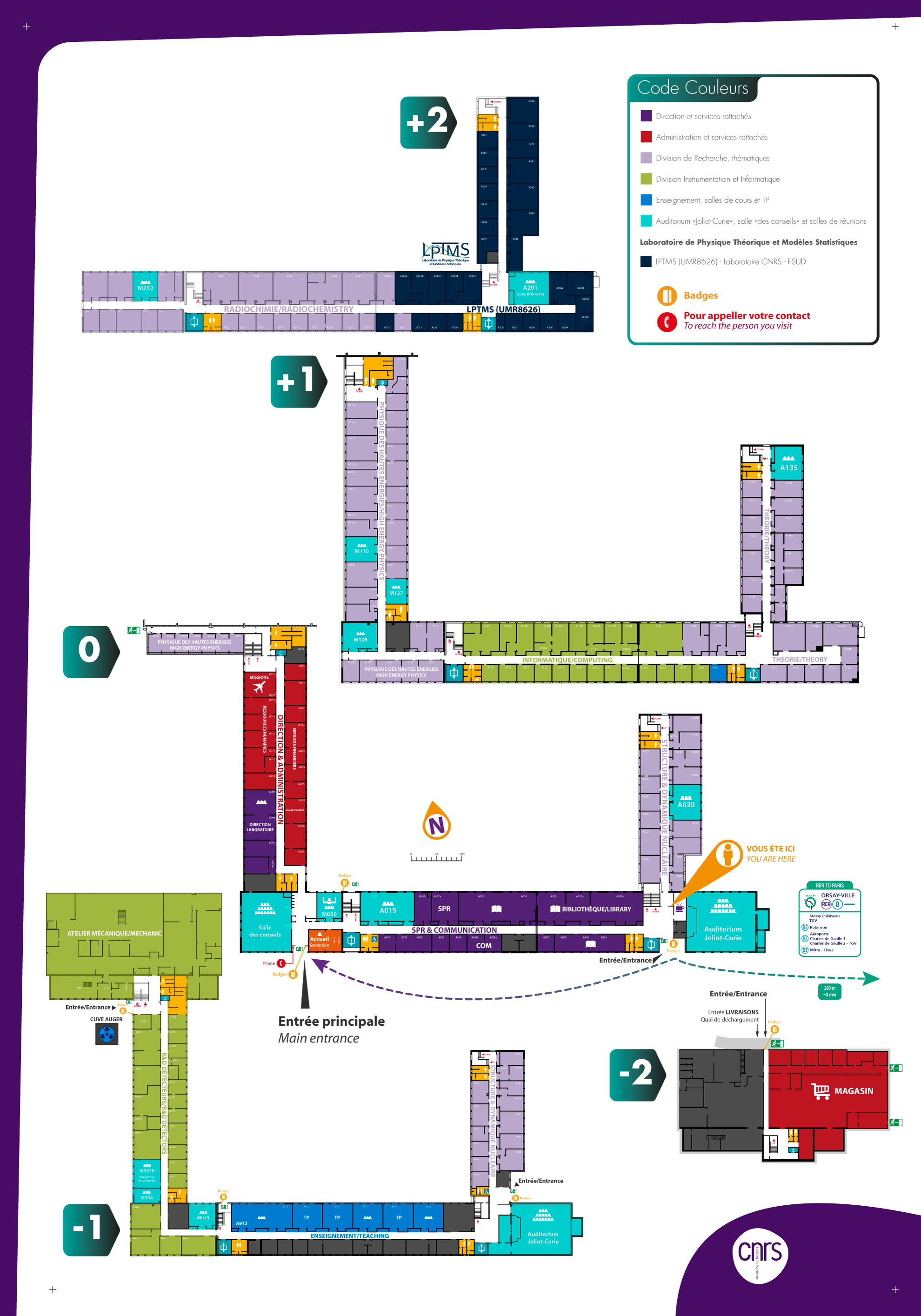
100/2-A201 - Salle A201 (IJCLab)

 

This work explores nuclear shape phase transitions through complementary theoretical frameworks. The Bohr-Mottelson model, based on the Bohr Hamiltonian, describes low-energy quadrupole states and nuclear deformations. Using analytical methods, new solutions are derived to reproduce experimental excitation energies and transition probabilities B(E2). The Interacting Boson Model (IBM) is applied to Ru isotopes, both with and without configuration mixing, to analyze shape evolution and coexistence.

 

Additionally, quantum computing techniques are used to investigate quantum phase transitions in finite systems via the Extended Lipkin Model (ELM), a simplified alternative to the IBM. Adaptive methods of pseudo-Trotter derived variational quantum optimizer assembly (ADAPT-VQE) enable its implementation on quantum platforms, while machine learning methods are explored for nuclear shape classification.

 

These results enhance our understanding of nuclear shape transitions, bridging theory and experiment while contributing to both nuclear physics and quantum technologies.

 

---

How to reach the seminar room:

Whereabouts of the laboratory on the Paris-Saclay campus

Bat. 100, general room map

Abstract_S_Baid.pdf